年金現価係数 | 複利計算に便利な6つの係数 | みつぞうの定年準備ブログ

年利ｒ%で複利運用しながら、将来のｎ年間にわたって毎年一定額を受け取るために必要な元本を求める係数を「年金現価係数」といいます。

定年退職後のじぶん年金を構築する場合、毎年受け取りたい年金額に対して必要な原資を計算するために使用できます。

取り崩し期間と年利から簡単に年金現価係数が求められる早見表が便利です。

年利ｒ％ → ｎ年運用 ↓	1%	2%	3%	4%	5%	6%	7%	8%	9%	10%
1 年	0.990	0.980	0.971	0.962	0.952	0.943	0.935	0.926	0.917	0.909
2 年	1.970	1.942	1.913	1.886	1.859	1.833	1.808	1.783	1.759	1.736
3 年	2.941	2.884	2.829	2.775	2.723	2.673	2.624	2.577	2.531	2.487
4 年	3.902	3.808	3.717	3.630	3.546	3.465	3.387	3.312	3.240	3.170
5 年	4.853	4.713	4.580	4.452	4.329	4.212	4.100	3.993	3.890	3.791
6 年	5.795	5.601	5.417	5.242	5.076	4.917	4.767	4.623	4.486	4.355
7 年	6.728	6.472	6.230	6.002	5.786	5.582	5.389	5.206	5.033	4.868
8 年	7.652	7.325	7.020	6.733	6.463	6.210	5.971	5.747	5.535	5.335
9 年	8.566	8.162	7.786	7.435	7.108	6.802	6.515	6.247	5.995	5.759
10 年	9.471	8.983	8.530	8.111	7.722	7.360	7.024	6.710	6.418	6.145
11 年	10.368	9.787	9.253	8.760	8.306	7.887	7.499	7.139	6.805	6.495
12 年	11.255	10.575	9.954	9.385	8.863	8.384	7.943	7.536	7.161	6.814
13 年	12.134	11.348	10.635	9.986	9.394	8.853	8.358	7.904	7.487	7.103
14 年	13.004	12.106	11.296	10.563	9.899	9.295	8.745	8.244	7.786	7.367
15 年	13.865	12.849	11.938	11.118	10.380	9.712	9.108	8.559	8.061	7.606
20 年	18.046	16.351	14.877	13.590	12.462	11.470	10.594	9.818	9.129	8.514
25 年	22.023	19.523	17.413	15.622	14.094	12.783	11.654	10.675	9.823	9.077
30 年	25.808	22.396	19.600	17.292	15.372	13.765	12.409	11.258	10.274	9.427

年金現価係数の早見表

使い方は簡単。毎年受け取りたい年金額に年金現価係数を掛けるだけです。

計算例：　年利5%で運用しながら毎年100万円を30年間取り崩すために必要な元本はいくら？

5%で30年間取り崩すときの年金終価係数：15.372

元本
＝ 100万円 × 15.372 ＝ 1537万円

つまり、上の例では約1537万円を年利5%で複利運用すれば、30年間にわたって毎年100万円を取り崩すことができることを示します。

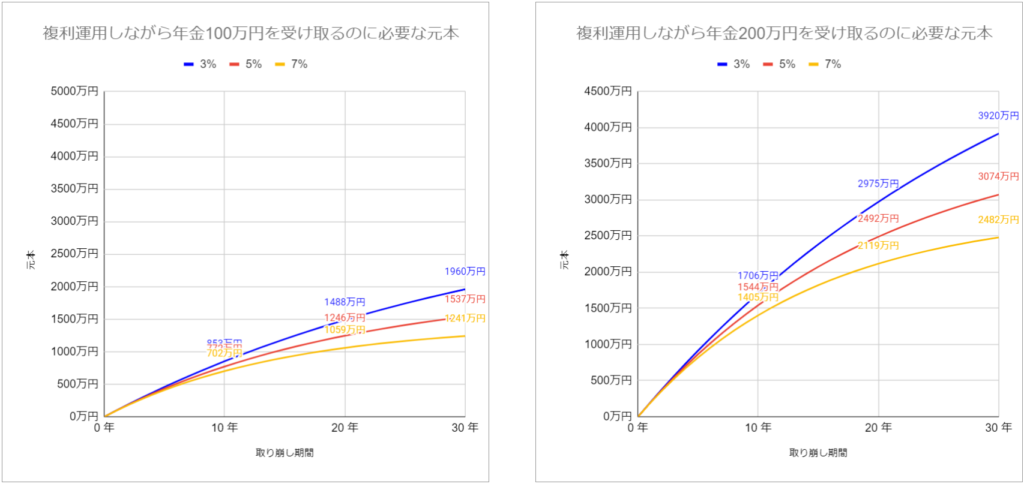
グラフに表すと次のようになります。

年金現価係数,年金現価係数とは,元本,グラフ,推移,複利,複利運用, ライフプラン, じぶん年金, 自分年金, 資産運用, ファイナンシャルプランナー, FP, FP2級, FP3級, 年利5%で複利運用ながら毎年100万円を受け取るのに必要な元本の推移 — 年利5%で複利運用ながら毎年100万円を受け取るのに必要な元本の推移

30年間にわたり毎年100万円を取り崩す場合、年利3%で運用すると元本は1960万円必要ですが、年利7%だと1241万円でよいことがわかります。

また、毎年の取り崩し額が200万円の場合は、年利3%で3920万円、年利5%で3074万円、年利7%では2482万円の元本が必要となります。

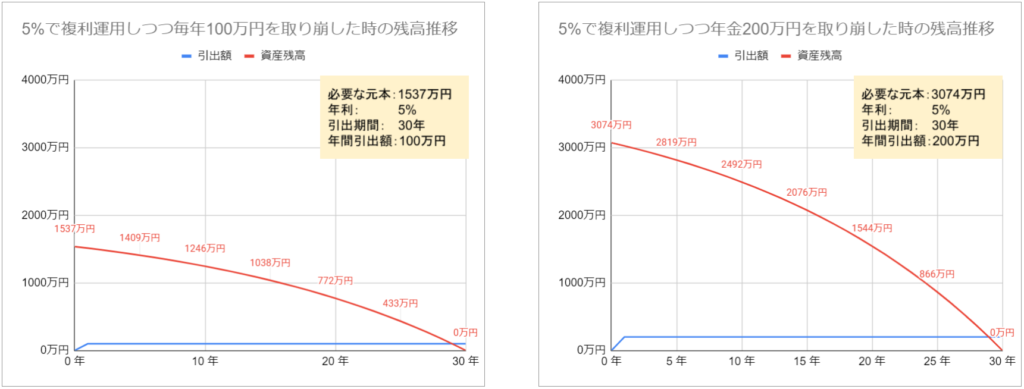
年金現価係数,年金現価係数とは,取り崩し残高,グラフ,推移,複利,複利運用, ライフプラン, じぶん年金, 自分年金, 資産運用, ファイナンシャルプランナー, FP, FP2級, FP3級, 年利5%で複利運用ながら毎年100万円を取り崩したときの残高推移 — 年利5%で複利運用ながら毎年100万円を取り崩したときの残高推移 | 年金現価係数

上のグラフは5%で運用しながら毎年100万円（または200万円）を30年間にわたって取り崩すときの、残高の推移です。

5%で複利運用することで残高の減少カーブは緩やかになり、確かに30年間にわたって毎年100万円（または200万円）を取り崩せ、30年目に残高がゼロになることが確認できます。

年金現価係数の求め方

必要な年金現価係数が早見表にないときは、次の計算式で求めることができます。

年金現価係数の計算式

$$\small{年金現価係数=\cfrac{(1+r)^n-1}{r (1+r)^n }}$$

　　　　r = 年利（％）
　　　　n = 積立年数

電卓で計算するときは、次のように入力すると計算できます。

電卓で計算するときの入力のしかた（年利r=５％で10年間の場合）

「(1+r)」を入力：
　　[1]　[+]　[0] [.] [0] [5]　[=]
「n乗」を入力：
　　[×]　[×]　[=] 　※「＝」を(年数－1)回入力
メモリーをクリアして、メモリーに保存：
　　[mc]　[m+]
「-1」を入力：
　　[－]　[1]　[=]
「÷r」を入力：
　　[÷]　[0] [.] [0] [5]
「÷(1+r)のn乗」を入力：
　　[÷]　[mr]　[=]